Bac de maths 2024 blanc n°4 : sujet et corrigé du baccalauréat.

🏆Sujets du Bac

Terminale • Lycée

Bac de maths 2024 blanc n°4

⏰ Durée : Variable

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Bac de maths 2024 blanc n°4 : sujet et corrigé du baccalauréat en PDF.
Un sujet portant sur les probabilités, les suites numériques, les équations paramétriques. Ainsi que, le logarithme népérien et la fonction exponentielle. Ce sujet qui dispose de sa correction permet aux élèves de réviser et de se préparer dans les meilleures conditions au baccalauréat de maths 2024 en terminale.

BACCALAURÉAT GÉNÉRAL
ÉPREUVE D’ENSEIGNEMENT DE SPÉCIALITÉ
SESSION 2024
MATHÉMATIQUES
Durée de l’épreuve : 4 heures
L’usage de la calculatrice avec mode examen actif est autorisé
L’usage de la calculatrice sans mémoire, « type collège » est autorisé.

Exercice 1 (5 points)

Partie A
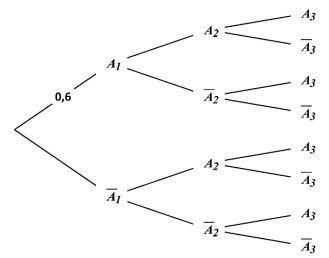
Un jeu proposé dans une fête foraine consiste à effectuer trois tirs successivement sur une cible
mouvante.

On a constaté que :
• Si le joueur atteint la cible lors d’un tir alors il ne l’atteint pas lors du tir suivant dans 65 %
des cas ;
• Si le joueur n’atteint pas la cible lors d’un tir alors il l’atteint lors du tir suivant dans 50 %
des cas.
La probabilité qu’un joueur atteigne la cible lors de son premier tir est de 0,6.
Pour tout événement A, on note P(A) sa probabilité et $\bar{A}$ l’événement contraire de A.
On choisit au hasard un joueur à ce jeu de tirs.

On considère les événements suivants :
• A1: « Le joueur atteint la cible lors du 1er tir »
• A2: « Le joueur atteint la cible lors du 2ème tir »
• A3: « Le joueur atteint la cible lors du 3ème tir ».

1. Recopier et compléter, avec les probabilités correspondantes sur chaque branche, l’arbre
pondéré ci-dessous modélisant la situation.

Soit X la variable aléatoire qui donne le nombre de fois où le joueur atteint sa cible au cours
des trois tirs.
2. Montrer que la probabilité que le joueur atteigne exactement deux fois la cible au cours des
trois tirs est égale à 0,4015.
3. L’objectif de cette question est de calculer l’espérance de la variable aléatoire X, notée
E(X).
a. Recopier et compléter le tableau ci-dessous donnant la loi de probabilité de la variable
aléatoire X.

b. Calculer E(X).
c. Interpréter le résultat précédent dans le contexte de l’exercice.

Partie B
On considère N, un entier naturel supérieur ou égal à 1.
Un groupe de N personnes se présente à ce stand pour jouer à ce jeu dans des conditions
identiques et indépendantes. Un joueur est déclaré gagnant lorsqu’il atteint trois fois la cible.
On note Y la variable aléatoire qui compte parmi les N personnes le nombre de joueurs déclarés
gagnants.
1. Dans cette question, N = 15.
a. Justifier que Y suit une loi binomiale dont on déterminera les paramètres.
b. Donner la probabilité, arrondie à $10^{-3}$ , qu’exactement 5 joueurs soient gagnants à ce
jeu.
2. Par la méthode de votre choix, que vous expliciterez, déterminer le nombre minimum de
personnes qui doivent se présenter à ce stand pour que la probabilité qu’il y ait au moins un
joueur gagnant soit supérieure ou égale à 0,98.

Exercice 2 (5 points)

Dans un repère orthonormé $(O,\vec{i},\vec{j},\vec{k})$ , on considère les points :
A(1 ; 1 ; −4), B(2 ; −1 ; −3), C(0 ; −1 ; −1) et $\Omega$ (1 ; 1 ; 2).
1. Démontrer que les points A, B, et C définissent un plan.
2. a. Démontrer que le vecteur $\vec{n}$ de coordonnées ;

est normal au plan (ABC).
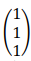
b. Justifier qu’une équation cartésienne du plan (ABC) est $x+ y+z + 2 = 0$ .
3. a. Justifier que le point $\Omega$ n’appartient pas au plan (ABC).

b. Déterminer les coordonnées du point H, projeté orthogonal du point $\Omega$ sur le plan (ABC).

On admet que $\Omega H = 2 \sqrt{3}$ .

On définit la sphère S de centre $\Omega$ et de rayon $\ 2 \sqrt{3}$ comme l’ensemble de tous les points M de l’espace tels que $\Omega H = 2 \sqrt{3}$ .
4. Justifier, sans calcul, que tout point N du plan (ABC), distinct de H, n’appartient pas à la
sphère S.
On dit qu’un plan $P$ est tangent à la sphère en un point K lorsque les deux conditions suivantes
sont vérifiées :
• $K\in P\cap S$
• $(\Omega K)\perp P$

5. Soit le plan $P$ d’équation cartésienne $x+y-z-6 = 0$ et le point K de coordonnées
K(3 ; 3 ; 0).

Démontrer que le plan $P$ est tangent à la sphère S au point K.
6. On admet que les plans (ABC) et $P$ sont sécants selon une droite ( $\Delta$ ).
Déterminer une équation paramétrique de la droite ( $\Delta$ ).

Exercice 3 (5 points)

Soit la suite ( $u_n$ ) définie par $u_0=0$ et, pour tout $n\in \mathbb{N}$ , $u_{n+1}=5u_n-8n+6$ .
1. Calculer $u_1$ et $u_2$ .
2. Soit $n$ un entier naturel.
Recopier et compléter la fonction suite_u d’argument n ci-dessous, écrite en langage
Python, afin qu’elle retourne la valeur de $u_n$ .

3. a. Démontrer par récurrence que, pour tout $n\in \mathbb{N}$ , $u_n\geq 2n$ .
b. En déduire la limite de la suite ( $u_n$ ).
c. Soit $p\in\mathbb{N}^*$ .

Pourquoi peut-on affirmer qu’il existe au moins un entier $n_0$ tel que, pour
tout entier naturel n vérifiant, $n\geq n_0$ , $u_n\geq 10^p$ ?
4. Démontrer que la suite ( $u_n$ ) est croissante.
5. On considère la suite ( $v_n$ ), définie pour tout $n\in \mathbb{N}$ , par $v_n=u_n-2n+1$ .

a. En dessous de la fonction suite_u précédente, on a écrit la fonction suite_v ci-dessous :

La commande « L.append » permet de rajouter, en dernière position, un élément dans
la liste L.
Lorsqu’on saisit suite_v(5) dans la console, on obtient l’affichage suivant :

Conjecturer, pour tout entier naturel $n$ , l’expression de $v_{n+1}$ en fonction de $v_n$ .
Démontrer cette conjecture.
b. En déduire, pour tout entier naturel $n$ , la forme explicite de $u_n$ en fonction de $n$ .

Exercice 4 (5 points)

Soit la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=ln(1+e^{-x})+\frac{1}{4}x$ .
On note $C_f$ la courbe représentative de la fonction $f$ dans un repère orthonormé $(O,\vec{i},\vec{j})$ du
plan.

Partie A
1. Déterminer la limite de $f$ en $+\infty$ .
2. On admet que la fonction $f$ est dérivable sur $\mathbb{R}$ et on note $f'$ sa fonction dérivée.
a. Montrer que, pour tout réel $x$ , $f'(x)=\frac{e^x-3}{4(e^x+1)}$ .
b. En déduire les variations de la fonction $f$ sur $\mathbb{R}$ .
c. Montrer que l’équation $f(x)=1$ admet une unique solution dans l’intervalle [2 ; 5].

Partie B
On admettra que la fonction $f'$ est dérivable sur $\mathbb{R}$ et pour tout réel $x$ , $f''(x)=\frac{e^x}{(1+e^x)^2}$ .On note $\Delta$ la tangente à la courbe $C_f$ au point d’abscisse 0.
Dans le graphique ci-dessous, on a représenté la courbe $C_f$ , la tangente $\Delta$ et le quadrilatère MNPQ
tel que M et N sont les deux points de la courbe $C_f$ d’abscisses respectives $\alpha$ et $-\alpha$ , et Q
et p sont les deux points de la droite $\Delta$ d’abscisses respectives $\alpha$ et $-\alpha$ .

1. a. Justifier le signe de $f''(x)$ pour $x\in\mathbb{R}$ .
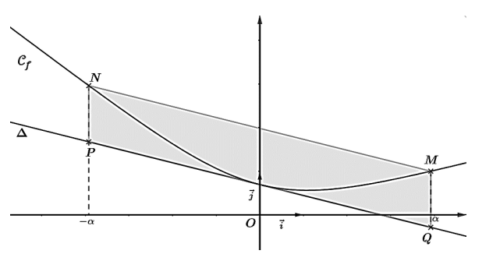
b. En déduire que la portion de la courbe $C_f$ , sur l’intervalle [− $\alpha$ ; $\alpha$ ], est inscrite dans le
quadrilatère MNPQ.
2. a. Montrer que $f(-\alpha )=ln(e^{-\alpha }+1)+\frac{3}{4}\alpha$ .b. Démontrer que le quadrilatère MNPQ est un parallélogramme.