Ce sujet dispose de son corrigé est peut être téléchargé ou imprimé en PDF.
L’épreuve porte sur les notions suivantes :
- Une étude de la paratuberculose avec des probabilités;
- Etude d’ne fonction contenant des logarithmes népériens et sa courbe ainsi que sa dérivée;
- Etude d’une suite numérique avec son sens de variation et sa convergence puis, un programme réalisé en Python;
- Un QCM avec l’équation paramétrique d’un plan, l’intersection de deux plans et l’utilisation du produit scalaire.
BACCALAURÉAT GÉNÉRAL
BAC BLANC MATHS 2024
Durée de l’épreuve : 4 heures
Exercice 1 (5 points)
La paratuberculose est une maladie digestive infectieuse qui touche les vaches. Elle est due à la
présence d’une bactérie dans l’intestin de la vache.
On réalise une étude dans une région dont 0,4% de la population de vaches est infectée.
Il existe un test qui met en évidence la réaction immunitaire de l’organisme infecté par la bactérie.
Le résultat de ce test peut être soit « positif », soit « négatif ».
On choisit une vache au hasard dans la région.
Compte tenu des caractéristiques du test, on sait que :
• Si la vache est atteinte par l’infection, la probabilité que son test soit positif est de 0,992 ;
• Si la vache n’est pas atteinte par l’infection, la probabilité que son test soit négatif est de
0,984.
On désigne par :
• I l’événement « la vache est atteinte par l’infection » ;
• l’événement « la vache présente un test positif ».
On note l’événement contraire de et
l’événement contraire de .
Les parties A et B sont indépendantes.
PARTIE A
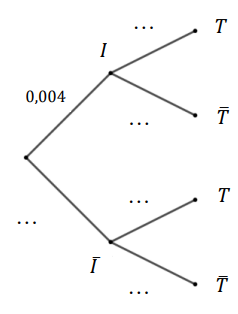
1. Reproduire et compléter l’arbre pondéré ci-dessous modélisant la situation.
2. a. Calculer la probabilité que la vache ne soit pas atteinte par l’infection et que son test soit
négatif. On donnera le résultat à près.
b. Montrer que la probabilité, à près, que la vache présente un test positif est environ
égale à 0,020.
c. La « valeur prédictive positive du test » est la probabilité que la vache soit atteinte par
l’infection sachant que son test est positif. Calculer la valeur prédictive positive de ce test.
On donnera le résultat à près.
d. Le test donne une information erronée sur l’état de santé de la vache lorsque la vache n’est
pas infectée et présente un résultat positif au test ou lorsque la vache est infectée et présente
un résultat négatif au test.
Calculer la probabilité que ce test donne une information erronée sur l’état de santé de la
vache. On donnera un résultat à près.
Partie B
3. Lorsqu’on choisit au hasard dans la région un échantillon de 100 vaches, on assimile ce choix
à un tirage avec remise.
On rappelle que, pour une vache choisie au hasard dans la région, la probabilité que le test
soit positif est égale à 0,02.
On note la variable aléatoire qui à un échantillon de 100 vaches de la région choisies au
hasard associe le nombre de vaches présentant un test positif dans cet échantillon.
a. Quelle est la loi de probabilité suivie par la variable aléatoire ? Justifier la réponse et
préciser les paramètres de cette loi.
b. Calculer la probabilité que dans un échantillon de 100 vaches, il y ait exactement 3
vaches présentant un test positif. On donnera un résultat à près.
c. Calculer la probabilité que dans un échantillon de 100 vaches, il y ait au plus 3 vaches
présentant un test positif. On donnera un résultat à 10−3 près.
4. On choisit à présent un échantillon de vaches dans cette région, étant un entier naturel non
nul. On admet que l’on peut assimiler ce choix à un tirage avec remise.
Déterminer la valeur minimale de pour que la probabilité qu’il y ait, dans l’échantillon, au
moins une vache testée positive, soit supérieure ou égale à 0,99.
Exercice 2 (5 points)
On considère la fonction définie sur l’intervalle par
, où ln
désigne la fonction logarithme népérien.
On admet que la fonction est deux fois dérivable sur .
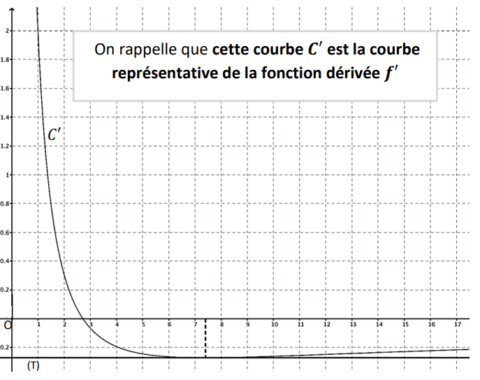
On note la courbe représentative de la fonction dans un repère orthogonal et ′ la courbe
représentative de la fonction ′, fonction dérivée de la fonction .
La courbe ′ est donnée ci-dessous ainsi que son unique tangente horizontale (T).
1. Par lecture graphique, avec la précision que permet le tracé ci-dessus, donner :
a. le coefficient directeur de la tangente à au point d’abscisse 1.
b. le plus grand intervalle sur lequel la fonction est convexe.
2. a. Calculer la limite de la fonction en .
b. Calculer . Interpréter graphiquement ce résultat.
3. Montrer que la courbe coupe l’axe des abscisses en deux points exactement dont on
précisera les coordonnées.
4. a. Montrer que pour tout réel appartenant à
,
.
b. En déduire, en justifiant, le tableau de variations de la fonction sur .
5. On note ′′ la dérivée seconde de et on admet que pour tout réel appartenant à ,
.
Déterminer par le calcul le plus grand intervalle sur lequel la fonction est convexe et préciser
les coordonnées du point d’inflexion de la courbe .
Exercice 3 (5 points)
On considère la suite définie par :
1. Calculer les valeurs exactes de et
. On détaillera les calculs.
2. On considère une fonction écrite en langage Python qui, pour un entier naturel donné, affiche
le terme . Compléter les lignes
et
de ce programme.
3. On admet que tous les termes de la suite sont strictement positifs.
a. Montrer que pour tout entier naturel non nul, on a : .
b. En déduire que la suite est décroissante.
c. La suite est-elle convergente ? Justifier votre réponse.
4. a. Montrer par récurrence que pour tout entier naturel non nul, on a : .
b. En déduire, si elle existe, la limite de la suite .
Exercice 4 (5 points)
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une
réponse exacte rapporte un point. Une réponse fausse, une réponse multiple ou l’absence de réponse
à une question ne rapporte ni n’enlève de point. Pour répondre, indiquer sur la copie le numéro de
la question et la lettre de la réponse choisie. Aucune justification n’est demandée.
L’espace est rapporté à un repère orthonormé .
On considère :
Les points (−1; −2; 3) , (1; −2; 7) et (1; 0; 2) ;
La droite Δ de représentation paramétrique :
le plan d’équation cartésienne : 3 + 2 + − 4 = 0 ;
le plan d’équation cartésienne : −6 − 4 − 2 + 7 = 0 .
Question 1 : Lequel des points suivants appartient au plan ?
a. (1; −3; 1) ; b. (1; 2; −1) ; c. (1; 0; 1) ; d. (2; −1; 1).
Question 2 : Le triangle est :
a. équilatéral ; b. rectangle isocèle ; c. isocèle non rectangle ; d. rectangle non isocèle.
Question 3 : La droite ∆ est :
a. orthogonale au plan ; b. sécante au plan ;
c. incluse dans le plan ; d. strictement parallèle au plan .
Question 4 : On donne le produit scalaire .
Une mesure au degré près de l’angle est :
a. 34° ; b. 120° ; c. 90° ; d. 0°.
Question 5 : L’intersection des plans et est :
a. un plan ; b. l’ensemble vide ; c. une droite ; d. réduite à un point.


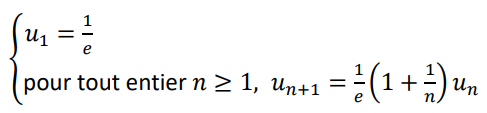

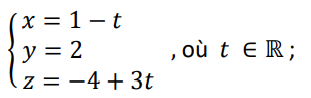






 Mathovore c'est 13 931 271 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 271 cours et exercices de maths téléchargés en PDF.