Arithmétique : cours de maths en terminale spécialité en PDF.
Mis à jour le 2 septembre 2025
I. Divisibilité.
Soient a et b deux entiers relatifs non nuls.
On dit que b divise a ou que a est divisible par b ou bien encore que a est un multiple de b
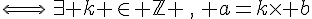
on note alors b/a .
Exemple :
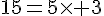
donc 5 divise 15, 3 divise 15, 15 est un multiple de 5 et de 3.
II. Propriétés.
Soient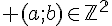 
.
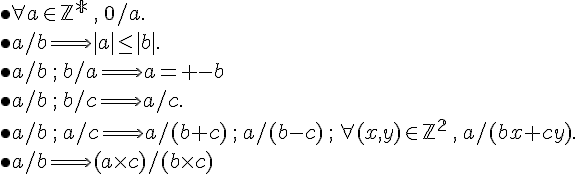
III. Définition.
Un entier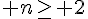 
est dit premier s’il n’admet dans 
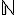aucun autre diviseur que lui-même et 1 .
Ensemble des nombres premiers
L’ensemble des nombres premiers, noté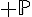 
est un ensemble infini.
.
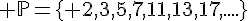IV. Théorème fondamental de l’arithmétique.
1. Décomposition en facteurs premiers.
Soit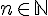 
.L’entier n se décompose de manière unique, à l’ordre près, sous forme de produit de nombres premiers.
.
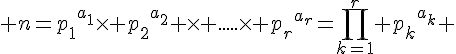2. Division euclidienne.
Soient a et b deux entiers relatifs tels que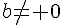 
alors Il existe un unique couple d’entiers (q,r) tel que :
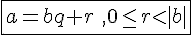
Remarque :
Que l’on soit dans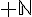 
ou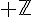 
, le reste r est toujours positif ou nul.
3. Congruences.
On dit que deux entiers relatifs sont congrus modulo n s’ils ont le même reste dans la division euclidienne par n.
Si c’est le cas, on note ![\fbox{a\equiv b [n]}](https://mathovore.fr/latex-images/d6c68568c5bf081f8cbacac27e26dcc6.png)
.
Exemple :
18=5×3+3 et 27=8×3+3.
18 et 27 ont le même reste (r=3) lors de la division euclidienne par 3
donc
![\fbox{27\equiv 18 [3]}](https://mathovore.fr/latex-images/4cf90905c600ff9f6fa8ec0246f4e68a.png)
![\bullet a\equiv b [n] \Longleftrightarrow a-b\equiv 0[n]\Longleftrightarrow \exists k\in \mathbb{N}\,,\,a-b=k\times n](https://mathovore.fr/latex-images/499ec61951c9e55d20ed1ec878d6d277.png)
![\bullet a\equiv b [n]\,;\, a\,#039;\equiv b\,#039; [n]\Longleftrightarrow a+a\,#039;\equiv b+b\,#039;[n] \ \Longleftrightarrow a\times a\,#039;\equiv b\times b\,#039;[n]\ \Longleftrightarrow a^p\equiv b^p[n] (p\in\mathbb{N})](https://mathovore.fr/latex-images/22ea249499fca1982030290bb04583f3.png)
4. Plus commun diviseur (pgcd) et plus petit commun multiple (ppcm) :
a. Definition du pgcd(a,b)
Soient a et b deux entiers relatifs.L’ensemble des diviseurs communs à a et b admet un plus grand élément nommé le pgcd(a,b).
On note aussi a^b.
b. Propriétés du pgcd(a,b)
Soit k un entier non nul.
Si k divise a et b alors :
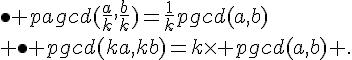
Remarque :
On peut déterminer le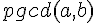 
de trois manières :
- par décomposition des deux nombres ;
- par une succession de divisions euclidiennes, le dernier reste non nul étant le pgcd(a,b) (théorème d’Euclide);
- par le théorème de Bézout (voir plus loin….)
c. Définition du ppcm(a, b).
Soient a et b deux entiers relatifs.
L’ensemble des multiples communs à a et b admet un plus petit élément nommé le ppcm(a,b).
On note aussi : a v b .
Soient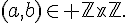 
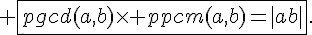
V. Théorème de Bézout :
Soit d= pgcd(a,b) alors il existe deux entiers relatifs u et v tels que :
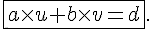
Deux nombres entiers a et b sont premiers entre eux si et seulement si pgcd(a,b)=1 .
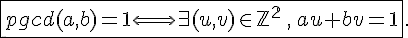
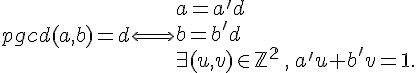
VI. Théorème de Gauss:
Si a divise bc et a premier avec b alors a divise c
Exemple :
5 divise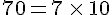 
or 5 est premier avec 7
donc d’après le théorème de Gauss 5 divise 10.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «arithmétique : cours de maths en terminale spécialité en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
